How To Draw A Fourbar Grashof Crank With Quick Return

7 .1. FOUR-BAR Mechanism

A iv-link machinery with four revolute joints is unremarkably chosen a 4-bar mechanism.

Application of iv-bar mechanisms to machinery is numerous. Some typical applications volition involve:

a) Correlation of the angular rotations of the links connected to the fixed link (commonly known as correlation of creepo angles or function generation ). In such applications we would like to accept a certain functional relation such as

q _xiv = f(q ₁₂) to exist realised past the four-bar mechanism. A simple example will exist to convert a linear scale to a logarithmic calibration within a certain range.

b) Link that has no connection to the fixed link is known equally the coupler link. A point on this link (which is known as the coupler point ) will describe a path on the stock-still link, which is chosen the coupler-point-curve . By proper choice of link dimensions useful curves, such as a straight-line or a circular arc, may be found. This coupler betoken bend can be used as the output of the four-bar machinery (such as the intermittent picture show drive shown below

c) The positions of the coupler-link may be used as the output of the 4-bar machinery. As shown in figure beneath, the four-bar mechanism used for the dump truck requires that the center of gravity of the dumper to move on an inclined straight line while it is beingness tilted (why?).

The above applications can be solved by the methods of synthesis which is beyond the topic. In this affiliate we shall talk over some basic characteristics of the four-bar.

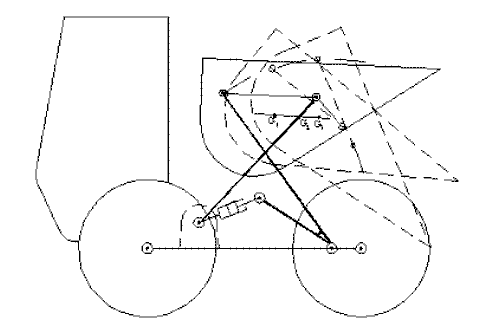
Dump truck

four.1.one. Grasshof's Theorem

The motion characteristics of a-four-bar machinery will depend on the ratio of the link length dimensions. The links that are connected to the stock-still link tin possibly have two different types of move:

i) The link may take a full rotation about the fixed axis (we call this blazon of link crank )

The link may oscillate (swing) between two limiting angles (we call this blazon of link rocker ).

In a four-bar mechanism we can have the post-obit three different types of movement:
i) Both of the links connected to the fixed link can have a full rotation. This type of four-bar is called "double-creepo " or " drag-link ".
2) Both of the links connected to the fixed link can only oscillate. This type of four-bar is chosen "double-rocker ."

iii) 1 of the links connected to the fixed link oscillates while the other has a full rotation. This blazon of four-bar is chosen creepo-rocker .

The type of movement is a function of the link lengths. Grashof'due south theorem (or Grashof's rule ) gives the criteria for these various conditions as follows:

Permit u.s.a. identify the link lengths in a four-bar chain as:

l= length of the longest link
southward= length of the shortest link
p,q = length of the two intermediate links

The following statements are valid (stated without proof. 1 can prove these statements past using the input-output equation of a four-bar Meet Appendix AIII for the proof of the theorem).
:
1. If l + s < p + q (if the sum of the lengths of the shortest and the longest links is less than the sum of the two intermediate links)

Then:

a, b) Ii different crank-rocker mechanisms are possible. In each example the shortest link is the crank, the stock-still link is either of the next links.

Ii different crank-rocker mechanisms

c) One double-crank (drag-link) is possible when the shortest link is the frame.

d) One double-rocker mechanism is possible when the link opposite the shortest link is the frame.

If l + s > p + q (if the sum of the longest and the shortest link lengths is greater than the sum of the lengths of the two intermediate links).

Only double-rocker mechanisms are possible (4 different mechanisms, depending on the fixed link).

If l + s = p + q the four possible mechanisms in (1) will result. However these mechanisms will suffer from a condition known equally the change signal. The eye lines of all the links are collinear at this position. The follower linkage may change the direction of rotation. This is an undetermined position.

four. i) A parallelogram linkage is a special case of (iii) where the reverse links are equal. All iv-possible mechanisms are double-crank suffering from the condition of change signal (Fig. 7.5a). It is possible to control the mechanisms at the modify bespeak past a configuration as shown

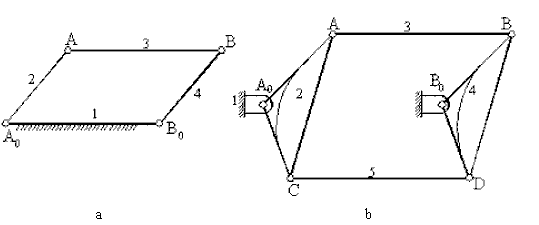
ii) A deltoid linkage is another special case of (3), in which two equal links are connected to ii equal longer links as shown in Fig. 7.6. With the long link as the frame a crank-rocker machinery is possible. The frame equally the short link may give a double-creepo mechanism, in which the short link may rotate twice while the long link as the follower will rotate once (this machinery is also known equally the Galloway mechanism which was patented in 1844) (Fig. 7.6.).

Note that if we multiply or divide all the link lengths past a constant, the ratio of the length of the links, hence the blazon of four-bar or the angular rotations of the links will not be effected. Therefore information technology is the ratio of the link lengths, not the link lengths as a whole, which determines the type of 4-bar. If our interest is the rotation of the links only, the mechanisms with the aforementioned link length ratios will have the same motion characteristics no thing how large or small the machinery is constructed (this scaling is like multiplying the loop equation by some constant).

Out of these types of iv-bar mechanisms crank-rocker mechanism has a item importance in car design since a continuous rotation may exist converted to an oscillation through this blazon of a iv-bar (this argument does not necessarily hateful that the other four-bar proportions are not used). We shall at present talk over the four-bar mechanism with crank-rocker proportions and important trouble related to it.

iv.1.2. Dead-Eye Positions of Creepo-Rocker Mechanisms
In crank-rocker mechanisms the rocker oscillates between ii limiting angles (In full general, the crank is the input and rocker is the output). The positions of the machinery when the rocker is at a limit position are chosen the dead-middle positions of the four-bar. We can also define the dead center position by considering the velocity of the rocker at these limiting angles. Since the rocker is moving in one direction before information technology reaches the limiting angle and since information technology moves in opposite direction after it passes this limit position, the velocity of the rocker at the limiting position must be nil. Hence, we can define a dead-center position as the position in which the rocker has instantaneously zero velocity. Consider a crank-rocker mechanism at an arbitrary position (Fig. 7.8). Assuming that the creepo is rotating with a speed w ₁₂, the angular velocity of the rocker is (refer to the velocity analysis of a four-bar machinery):

From this equation we tin state that the rocker angular velocity volition be zero when sin(q ₁₂-q _xiii)=0 or when q ₁₂-q ₁₃=0 or p. At these positions the coupler and creepo angles are equal or differ by p (The coupler and the crank are collinear- along the aforementioned line in extended or folded position). Hence we obtain the two limiting positions of the rocker as shown below.

Extended dead-center position is when the creepo and the coupler links are extended (q ₁₂=q ₁₃) and folded dead-middle position is when the crank and the coupler are folded on peak of each other (q ₁₃=q ₁₂+p). The oscillation angle of the rocker between the dead-center positions and measured from the extended dead-centre to the folded dead-middle position is chosen the swing bending , y. There is a corresponding crank rotation, f. Sometimes, rather than the corresponding crank bending, time-ratio between the forward and reverse oscillations (strokes) is used. If we assume that the creepo is rotating at a constant speed, we define the fourth dimension ratio every bit:

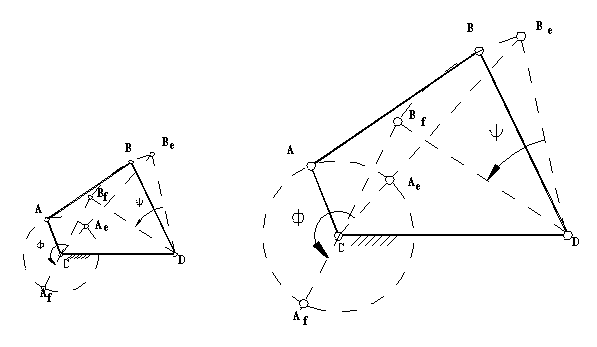
Forward stroke of the rocker is when the rocker is moving from extended to folded dead-center position in counterclockwise management (In mechanism frontwards stroke is the management of movement during which the rocker is doing piece of work. This definition need not correspond to the kinematic definition given above).
In case of four-bar mechanisms with crank-rocker proportions, if we accept the mirror image of the mechanism with respect to the fixed link, we obtain some other four bar machinery of crank-rocker proportions and the same swing angle, y. However, when the crank rotates from the extended dead center position to the folded position in counter-clockwise management the rocker will rotate in clockwise management and the creepo rotation is 360⁰- f.
The reason why the limiting position is called the expressionless-centre position is that when the machinery is at this position and if there is a forcefulness practical to the rocker, the machinery will not move, e.g. the mechanism is locked with respect to an input movement or force from the rocker. This characteristics may sometimes be very useful.

4.1.3. Transmission Angle

It is rather important to understand how the mechanism will function under loaded conditions in practice while the kinematic characteristics of the machinery is being considered. Past the performance of the machinery we mean the effective transmission of motion (and force) from the input link to the output link. This besides ways that for a constant torque input, in a well performing mechanism nosotros must obtain the maximum torque output that is possible and the bearing forces must be a minimum. Of course, torque and forcefulness are not the quantities that has been in the kinematics and any kinematic quantity nosotros use to ascertain the performance of the mechanism, this quantity volition merely judge the static force characteristics of the mechanism. The dynamic characteristics, which is a office of mass and moment of inertia of the rigid bodies, may be several times more than the static forces and the behaviour of the mechanism under the dynamic forces cannot be predicted past kinematics. Yet, some rule-of-pollex of the behaviour of the machinery under load is better and so none. Alt divers the manual angle as:

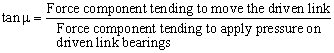
or, the transmission angle can be defined as:

Below the transmission angle for a 4-bar machinery and for a slider-crank mechanisms are shown. It is a simple parameter in which neither the forces nor the velocities are taken into consideration. Notwithstanding, 1 tin can gauge the performance of the machinery in the kinematic design phase.

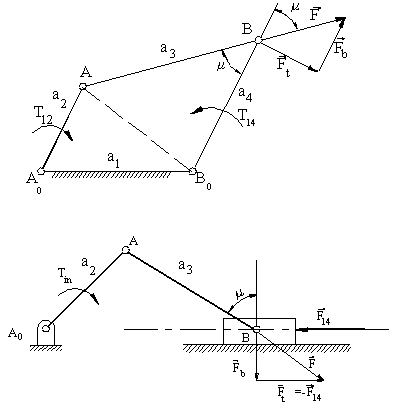
Clearly, the optimum value of the transmission angle is xc⁰. Since the angle will be constantly changing during the movement cycle of the machinery, at that place will exist a position at which the transmission bending volition deviate most from ninety⁰. In exercise it has been found out that if the maximum deviation of the transmission bending from xc⁰ exceeds forty⁰ or 50⁰ (depending on the type of awarding), the mechanism will lock. In certain cases this maximum departure must be kept within xx⁰ (e.chiliad. reciprocating pumps) and in certain other applications maximum deviations of up to 70⁰ may be permissible (e.g. shipping landing gears). I must consider the applied awarding of a machinery in gild to requite a limit to this difference (whenever in doubtfulness, try to keep this difference to less that 40⁰ or fifty⁰).

One can express the manual bending in terms of the crank angle and the link lengths as (by writing the cosine theorem for AB₀ using the triangles A₀AB₀ and ABB₀ and equating the length AB₀).

(1)
or

(2)

The minimum and the maximum of the transmission angle can exist determined by taking the derivative of the equation (2) with respect to q ₁₂ and equating to zero:

(3)

The minimum and the maximum values of the transmission angle will be when sin(q ₁₂)=0 or when q ₁₂=0 or p (when the crank and the stock-still link are collinear in extended or folded positions). The minimum and the maximum value of the transmission angle for the four-bar mechanism will be given past:

(four)

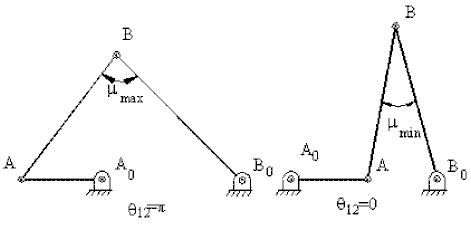
The disquisitional transmission bending is either mmin or mmax, whichever deviates nearly from 90⁰ . Sometimes, for the transmission angles greater than ninety⁰, instead of m (180⁰-g) is used for the value of the transmission bending. In such a case, there are two minimum values of the transmission angle ( m _min1=grand _min, k _min2=180⁰-m _max) The most critical transmission angle is the minimum of k _min1 and m _min2. Note that the deviation of the transmission angle from 90⁰ at the two extreme positions will be equal if:

(v)

Such four-bar mechanisms are known as centric four-bar . In axial 4-bar mechanisms the fourth dimension ratio is unity (the crank rotation between dead-centers is 180⁰) and they will take a better force transmission characteristics as compared with the other crank-rocker proportions.

Example iv.1.

Determine the swing angle, corresponding creepo rotation and the maximum deviation of the manual angle from 90⁰ for the iv-bar machinery whose link lengths are: a₂=4, a₃=8, a_iv=six, a₁=7.

Since the sum of the longest and the shortest link lengths (4+eight=12) is less and then the lengths of the 2 intermediate links (six+7=13) the mechanism is of crank-rocker type and link 2 is the crank. At the expressionless eye positions since the crank and the coupler links are collinear, the iv-bar machinery is of triangular form.
Applying the cosine theorem for the extended dead centre: